Quantum state exclusion

In this tutorial, we are going to cover the problem of quantum state exclusion. We are going to briefly describe the problem setting and then describe how one may use |toqito⟩ to calculate the optimal probability with which this problem can be solved for a number of different scenarios.

Quantum state exclusion is very closely related to the problem of quantum state distinguishability. It may be useful to consult the Quantum state distinguishability tutorial on this topic.

Further information beyond the scope of this tutorial can be found in the text :footcite:Pusey_2012_On as well as the course [1].

The state exclusion problem

The quantum state exclusion problem is phrased as follows.

1. Alice possesses an ensemble of \(n\) quantum states:

   \[\begin{equation} \eta = \left( (p_0, \rho_0), \ldots, (p_n, \rho_n) \right), \end{equation}\]

   where \(p_i\) is the probability with which state \(\rho_i\) is selected from the ensemble. Alice picks \(\rho_i\) with probability \(p_i\) from her ensemble and sends \(\rho_i\) to Bob.

2. Bob receives \(\rho_i\). Both Alice and Bob are aware of how the ensemble is defined but he does not know what index \(i\) corresponding to the state \(\rho_i\) he receives from Alice is.

3. Bob wants to guess which of the states from the ensemble he was not given. In order to do so, he may measure \(\rho_i\) to guess the index \(i\) for which the state in the ensemble corresponds.

This setting is depicted in the following figure.

The quantum state exclusion setting.

Note

The primary difference between the quantum state distinguishability scenario and the quantum state exclusion scenario is that in the former, Bob want to guess which state he was given, and in the latter, Bob wants to guess which state he was not given.

Perfect state exclusion (antidistinguishability)

We say that if one is able to perfectly (without error) exclude all quantum states in a set, then the set of states is antidistinguishable.

Definition: Let \(n\) and \(d\) be integers. A collection of quantum states \(S = \{|\psi_1\rangle, \ldots, |\psi_{n}\rangle\} \subset \mathbb{C}^d\) are antidistinguishable if there exists a collection of positive operator value measurements \(\{M_1, \ldots, M_{n}\}\) such that \(\langle \psi_i | M_i | \psi_i \rangle = 0\) for all \(1 \leq i \leq n\).

Recall that a collection of POVMs are positive semidefinite operators \(\{M_i : 1 \leq i \leq n\} \subset \mathbb{C}^d\) that satisfy

\[\begin{equation} \sum_{i=1}^{n} M_i = \mathbb{I}_{d}. \end{equation}\]

Properties:

• If \(S\) is distinguishable then it is antidistinguishable.

• If \(n = 2\) then \(S\) is distinguishable if and only if \(S\) is antidistinguishable.

  • Distinguishing one state from a pair of states is equivalent to excluding one of the states from that pair.

• If \(n \geq 3\) then there are antidistinguishable sets that are not distinguishable.

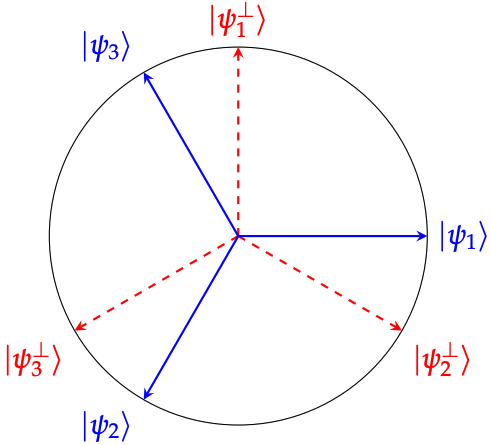
Example: Trine states

The so-called trine states are a set of three states, each of dimension two defined as

\[\begin{equation} |\psi_1\rangle = |0\rangle, \quad |\psi_2\rangle = -\frac{1}{2}(|0\rangle + \sqrt{3}|1\rangle), \quad |\psi_3\rangle = -\frac{1}{2}(|0\rangle - \sqrt{3}|1\rangle). \end{equation}\]

from toqito.states import trine

psi1, psi2, psi3 = trine()
print(f"|𝛙_1> = {psi1.reshape(1, -1)[0]}")
print(f"|𝛙_2> = {psi2.reshape(1, -1)[0]}")
print(f"|𝛙_3> = {psi3.reshape(1, -1)[0]}")

|𝛙_1> = [1 0]
|𝛙_2> = [-0.5       -0.8660254]
|𝛙_3> = [-0.5        0.8660254]

The trine states are three states in two dimensions. So they can’t be mutually orthogonal, but they are about “as close as you can get” for three states in two dimensions to be mutually orthogonal.

from toqito.states import trine
from toqito.state_props import is_mutually_orthogonal

print(f"Are states mutually orthogonal: {is_mutually_orthogonal(trine())}")

Are states mutually orthogonal: False

An interesting property of these states is that they are antidistinguishable but not distinguishable.

from toqito.states import trine
from toqito.state_props import is_distinguishable, is_antidistinguishable

print(f"Trine antidistinguishable: {is_antidistinguishable(trine())}")
print(f"Trine distinguishable: {is_distinguishable(trine())}")

Trine antidistinguishable: True
Trine distinguishable: False

Here are a set of measurements that we can verify which satisfy the antidistinguishability constraints. We will see a method that we can use to obtain these directly later.

\[\begin{equation} M_1 = \frac{2}{3} (\mathbb{I} - |\psi_1\rangle \langle \psi_1|), \quad M_2 = \frac{2}{3} (\mathbb{I} - |\psi_2\rangle \langle \psi_2|), \quad M_3 = \frac{2}{3} (\mathbb{I} - |\psi_3\rangle \langle \psi_3|). \end{equation}\]

import numpy as np

M1 = 2 / 3 * (np.identity(2) - psi1 @ psi1.conj().T)
M2 = 2 / 3 * (np.identity(2) - psi2 @ psi2.conj().T)
M3 = 2 / 3 * (np.identity(2) - psi3 @ psi3.conj().T)

In order for \(M_1\), \(M_2\), and \(M_3\) to constitute as valid POVMs, each of these matrices must be positive semidefinite and we must ensure that \(\sum_{i \in \{1,2,3\}} M_i = \mathbb{I}_2\).

from toqito.matrix_props import is_positive_semidefinite

print(f"M_1 + M_2 + M_3 is identity: {np.allclose(M1 + M2 + M3, np.identity(2))}")
print(f"Is M_1 PSD: {is_positive_semidefinite(M1)}")
print(f"Is M_2 PSD: {is_positive_semidefinite(M2)}")
print(f"Is M_3 PSD: {is_positive_semidefinite(M3)}")

M_1 + M_2 + M_3 is identity: True
Is M_1 PSD: True
Is M_2 PSD: True
Is M_3 PSD: True

Next, we must show that these measurements satisfy \(\langle \psi_i | M_i | \psi_i \rangle = 0\) for all \(i \in \{1,2,3\}\).

print(f"<𝛙_1| M_1 |𝛙_1>: {np.around((psi1.reshape(1, -1)[0] @ M1 @ psi1)[0], decimals=5)}")
print(f"<𝛙_2| M_2 |𝛙_2>: {np.around((psi2.reshape(1, -1)[0] @ M2 @ psi2)[0], decimals=5)}")
print(f"<𝛙_3| M_3 |𝛙_3>: {np.around((psi3.reshape(1, -1)[0] @ M3 @ psi3)[0], decimals=5)}")

<𝛙_1| M_1 |𝛙_1>: 0.0
<𝛙_2| M_2 |𝛙_2>: 0.0
<𝛙_3| M_3 |𝛙_3>: 0.0

Since we have exhibited a set of measurements \(\{M_i: i \in \{1,2,3\}\} \subset \text{Pos}(\mathbb{C^d})\) that satisfy

\[\begin{equation} \langle \psi_i | M_i | \psi_i \rangle = 0 \quad \text{and} \quad \sum_{i \in \{1,2,3\}} M_i = \mathbb{I}_2 \end{equation}\]

for all \(i\), we conclude that the trine states are antidistinguishable.

An SDP for antidistinguishability

Whether a collection of states \(\{|\psi_1 \rangle, |\psi_2\rangle, \ldots, |\psi_{n}\rangle \}\) are antidistinguishable or not can be determined by the following semidefinite program (SDP).

\[\begin{split}\begin{equation} \begin{aligned} \text{minimize:} \quad & \sum_{i=1}^{n} \langle \psi_i | M_i | \psi_i \rangle \\ \text{subject to:} \quad & \sum_{i=1}^{n} M_i = \mathbb{I}_{\mathcal{X}}, \\ & M_i \succeq 0 \quad \forall \ 1 \leq i \leq n. \end{aligned} \end{equation}\end{split}\]

Consider again the trine states from the previous example. We can determine that they are antidistinguishable by way of the antidistinguishability SDP.

from toqito.states import trine
from toqito.state_opt import state_exclusion

opt_value, measurements = state_exclusion(trine(), probs=[1, 1, 1], primal_dual="dual")
print(f"Optimal SDP value: {np.around(opt_value, decimals=2)}")

Optimal SDP value: 0.0

The SDP not only gives us the optimal value, which is $0$ in this case, indicating that the states are antidistinguishable, but we also get a set of optimal measurement operators. These should look familiar to the measurements we explicitly constructed earlier.

Antidistinguishability and \((n-1)\)-incoherence

Antidistinguishability of a set of pure states is equivalent to a certain notion from the theory of quantum resources referred to as \(k\)-incoherence [2]:

Definition: Let \(n\) and \(k\) be positive integers. Then \(X \in \text{Pos}(\mathbb{C} ^n)\) is called \(k\)-incoherent* if there exists a positive integer \(m\), a set \(S = \{|\psi_0\rangle, |\psi_1\rangle,\ldots, |\psi_{m-1}\rangle\} \subset \mathbb{C} ^n\) with the property that each \(|\psi_i\rangle\) has at most \(k\) non-zero entries, and real scalars \(c_0, c_1, \ldots, c_{m-1} \geq 0\) for which

\[X = \sum_{j=0}^{m-1} c_j |psi_j\rangle \langle \psi_j|.\]

It turns out that antidistinguishability is equivalent to \(k\)-incoherence in the \(k = n - 1\) case. Reproducing one of the results from [3], we have the following theorem.

Theorem: Let \(n \geq 2\) be an integer and let \(S = \{|\phi_0\rangle, |\phi_1\rangle, \ldots, |\phi_{n-1}\rangle\}\). Then \(S\) is antidistinguishable if and only if the Gram matrix \(G\) is \((n-1)\)-incoherent.

\[\begin{split}G = \begin{pmatrix} 1 & \langle \phi_0 | \phi_1 \rangle & \cdots & \langle \phi_0 | \phi_{n-1}\rangle \\ \langle \phi_1 | \phi_0 \rangle & 1 & \cdots & \langle \phi_1 | \phi_{n-1}\rangle \\ \vdots & \vdots & \ddots & \vdots \\ \langle \phi_{n-1} | \phi_0 \rangle & \langle \phi_{n-1} | \phi_1 \rangle & \cdots & 1 \end{pmatrix}\end{split}\]

As an example, we can generate a random collection of quantum states, obtain the corresponding Gram matrix, and compute whether the set of states are antidistinguishable and \((n-1)\)-incoherent.

from toqito.state_props import is_antidistinguishable
from toqito.matrix_ops import vectors_to_gram_matrix
from toqito.matrix_props import is_k_incoherent
from toqito.rand import random_states

n, d = 3, 3
states = random_states(n, d)
gram = vectors_to_gram_matrix(states)

print(f"Is Antidistinguishable: {is_antidistinguishable(states)}")
print(f"Is (n-1)-incoherent: {is_k_incoherent(gram, n - 1)}")

Is Antidistinguishable: False
Is (n-1)-incoherent: False

As can be seen, whether the random set of states are antidistinguishable or not aligns with whether they are \((n-1)\)-incoherent or not as well.

References

[1]

Somshubhro Bandyopadhyay, Rahul Jain, Jonathan Oppenheim, and Christopher Perry. Conclusive exclusion of quantum states. Physical Review A, Feb 2014. URL: http://dx.doi.org/10.1103/PhysRevA.89.022336, doi:10.1103/physreva.89.022336.

[2]

Nathaniel Johnston, Shirin Moein, Rajesh Pereira, and Sarah Plosker. Absolutely k-incoherent quantum states and spectral inequalities for the factor width of a matrix. Physical Review A, 106(5):052417, 2022.

[3]

Nathaniel Johnston, Vincent Russo, and Jamie Sikora. Tight bounds for antidistinguishability and circulant sets of pure quantum states. Quantum, 9:1622, 2025.